Mes: enero 2018

1. Historia de las teorías de la unificación

Para saber por qué la física moderna ha llegado a un callejón sin salida, tenemos que retroceder a mediados del siglo XIX.

En aquel tiempo, se conocían tres tipos de fuerzas en el Universo: la gravedad, la electricidad y el magnetismo. Toda fuerza en el universo podía reducirse a uno de estos tres tipos de fuerzas.

Así, por ejemplo, cuando uno sostiene una piedra con la mano, hay una fuerza para abajo (la gravedad de la Tierra) y una fuerza para arriba (la oposición eléctrica entre los electrones de la mano y los electrones de la piedra), que se cancelan exactamente por ser de la misma intensidad y sentido opuesto, por lo que la piedra permanece inmóvil.

Cada uno de estos tres tipos de fuerzas tenía sus propias ecuaciones (en caso de la gravedad, las ecuaciones de Newton) y sus propias características.

La historia comienza en 1865, cuando el científico James Clerk Maxwell publica un conjunto de ecuaciones que gobiernan al mismo tiempo la electricidad y el magnetismo. Con ellas demuestra que la electricidad y el magnetismo no son dos tipos de fuerzas diferentes sino las dos caras de un mismo tipo de fuerza: el electromagnetismo, que se expresa en ciertas ocasiones como electricidad y en otras ocasiones como magnetismo.

Además, las ecuaciones definían la existencia de ondas electromagnéticas que, más tarde, se identificaron con la luz, tanto visible (rojo, azul, violeta, etc) como invisible (infrarrojo, ultravioleta, microondas, ondas de radio, etc). Así que, de carambola, Maxwell explicó la naturaleza de la luz.

Esto fue un avance revolucionario (un enorme «breakthrough», Miquel). De las ecuaciones de Maxwell se deriva toda la electrónica, informática y comunicación modernas. Cada vez que sostienes el iPhone en tus manos compruebas el inmenso poder de esas ecuaciones para crear artefactos insuperables.

Así, después de la unificación de Maxwell, quedaron dos fuerzas en el universo: la gravedad (regida por la teoría de Newton) y el electromagnetismo (regida por la teoría de Maxwell).

Durante la primera mitad del siglo XX aparecieron dos teorías matemáticas que explicaban mejor el comportamiento de estos dos tipos de fuerzas. Para la gravedad, apareció la relatividad general de Einstein. Para el electromagnetismo, apareció la física cuántica (con gente como Planck, Schrödinger, Heisenberg, Max Born y el mismo Einstein, que fue uno de sus pioneros y su mayor oponente). Las teorías de Newton y de Maxwell siguieron siendo aplicables para la inmensa mayoría de los casos cotidianos, pero las nuevas teorías explicaban mejor los casos no cotidianos, por lo que pueden considerarse una generalización de las teorías antiguas.

Ahora bien, mucha gente (entre la que me incluyo) considera sumamente desagradable que existan dos tipos de fuerzas diferentes y dos teorías diferentes que las rigen. Por tres razones:

• Para comenzar, ¿por qué dos tipos de fuerzas? Dos es un número realmente feo y poco elegante. Uno es el número más elegante, más sencillo desde el punto de vista matemático.
• ¿Por qué dos teorías diferentes? La realidad física es sólo una y única. ¿Por qué necesitamos dos teorías para explicarla?
• Para más inri, la relatividad general y la física cuántica son teorías incompatibles. No pueden ser las dos ciertas a la vez (pero sí pueden ser las dos falsas a la vez). Es sumamente desagradable que para explicar la realidad tengamos que usar dos teorías incompatibles entre ellas, cuando la realidad física es única y compatible con ella misma.

¿No sería posible unificar las dos fuerzas en una sola teoría con un conjunto único de ecuaciones, de la misma forma que hizo Maxwell con la electricidad y el magnetismo? Si así fuera, la gravedad y el electromagnetismo no serían dos tipos de fuerza sino dos caras del mismo tipo de fuerzas, con una sola teoría.

Eso sería mucho más elegante y bonito. Tendríamos una «teoría del todo», una teoría que explicaría toda la física. Una realidad, un tipo de fuerza, una teoría. Un anillo para gobernarlos a todos.

Como decían los antepasados, «el camino al infierno está empedrado de buenas intenciones». Esa bella idea de unificar todas las fuerzas en una sola teoría iba a ser el agujero negro que se iba a tragar toda la Física moderna.

El primero que cayó en este agujero fue Einstein, que pasó la segunda parte de su vida buscando esa teoría que unificaría el electromagnetismo con la gravedad, fallando estrepitosamente.

Más adelante, se descubrieron en el Universo dos tipos de fuerzas adicionales: la fuerza nuclear fuerte y la fuerza nuclear débil (las cuales operan en el núcleo del átomo). Ahora no teníamos que unificar dos fuerzas sino cuatro. El problema se hizo más difícil. También más importante, porque 4 es un número más feo que 2.

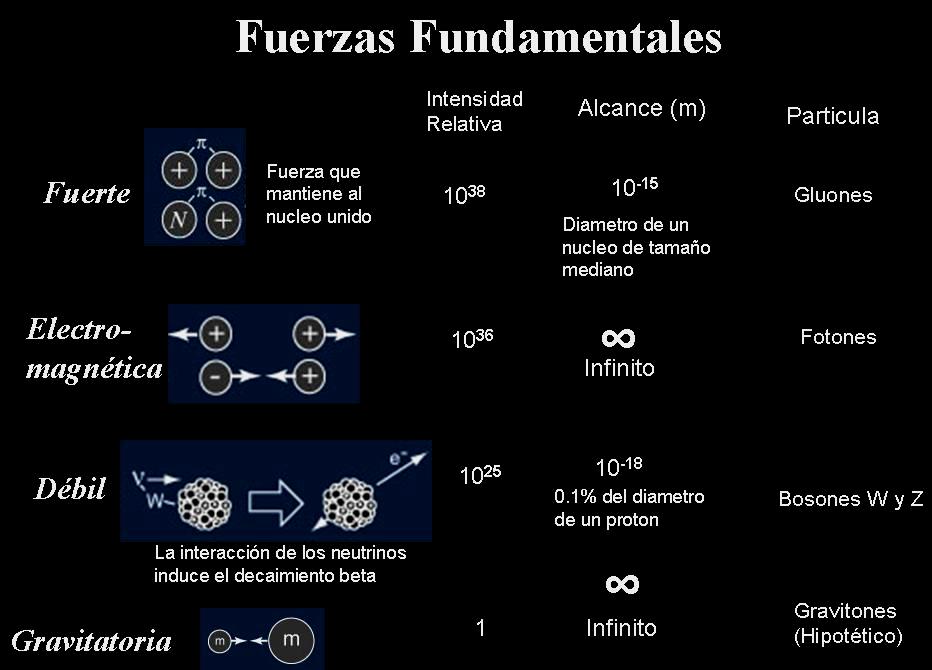
La cosa comenzó progresando con un ritmo razonable. Usando algunos trucos matemáticos, los científicos encontraron una manera de unificar la fuerza electromagnética con la fuerza nuclear débil como dos caras de la misma fuerza, que llamaron «electrodébil». La teoría fue comprobada con experimentos. Por ello, Sheldon Glashow, Abdus Salam y Steven Weinberg recibieron el Premio Nobel de Física de 1979.

Cuando yo comenzaba a leer de estos temas durante los años 80, los libros de divulgación científica tenían un tono optimista: era sólo cuestión de tiempo que se formulara una teoría que unificara  las tres fuerzas: gravedad, fuerte y electrodébil en una sola. Así llegaríamos a la «teoría del todo», el Santo Grial de la Física Moderna.

De varias candidatas para la teoría del todo, la más prometedora parecía la teoría de cuerdas («string theory»). Según esta teoría, las partículas elementales (electrón, fotón, quarks, etc) no eran en realidad puntos, sino líneas que vibraban a diferentes ritmos y en diferentes formas (a las que se llamó «cuerdas»). Esas cuerdas vibrantes producían las partículas tal como las conocíamos y, en última instancia, todo el mundo físico. Las ecuaciones derivadas de la vibración de las cuerdas tendrían la posibilidad de unificar las tres fuerzas, es decir, la teoría de cuerdas sería la «teoría del todo».

Fue una época de gran optimismo. Todos estaban convencidos de que se iba a conseguir la teoría definitiva que explicaría el Universo y que sería el logro mayor de la historia de la Física. Una única teoría explicaría todo el Universo de una forma bella y elegante. Algunos incluso profetizaron que, después de esta unificación, sólo quedarían detalles menores por investigar en Física. Aclarados estos detalles, la Física acabaría como ciencia porque nada quedaría por explicar: todo estaría explicado con un esquema racional y bellísimo.

Y entonces, todo comenzó a ir de mal en peor.

2. Intentando solucionar el problema más difícil de todos

Este bello panorama se enfrentaba con un obstáculo muy difícil de salvar.

Para comprobar la teoría de cuerdas u otras teorías unificadoras de fuerza, se necesitaban energías enormes. Alguien calculó que el acelerador de partículas que se necesitaría para hacer los experimentos era tan grande como el sistema solar.

Esto colocó a la Física en un problema. ¿Cómo comprobar esas nuevas teorías si los experimentos para comprobarlas o descartarlas no podían llevarse a cabo?

La estrategia más obvia era ponerse a investigar nuevas técnicas para crear aceleradores de partículas más potentes, que no necesitaran ser tan grandes como el Sistema Solar pero que produjeran los mismos efectos. Pero esto es más fácil decirlo que hacerlo: a veces la tecnología encuentra límites difíciles de franquear (por ejemplo, los aviones de hoy viajan a la misma velocidad que los de hace 50 años y, con toda seguridad, a la misma velocidad que los aviones que viajarán 50 años en el futuro).

Además, la estrategia de pasar de concentrarse en ecuaciones a  concentrarse en tecnología de aceleradores de partículas choca con prejuicios muy arraigados en la ciencia occidental, prejuicios que vienen de los antiguos griegos.

En efecto, en el tiempo de los griegos, no existía todavía la ciencia, pero sí existía la filosofía natural (la parte de la filosofía dedicada al mundo natural), que es el antepasado de la ciencia. El problema de la filosofía natural durante los tiempos griegos y helenísticos fue que la teoría se consideraba noble y admirable mientras que mancharse en las manos con los experimentos se consideraba poco digno. Esto era el reflejo de una sociedad en que a los pobres se les consideraba chusma despreciable (el amor por los pobres llegaría después, con el cristianismo), el trabajo manual lo hacían los despreciables esclavos y los únicos que tenían tiempo para el trabajo intelectual era la gente con recursos económicos, que se consideraban demasiado nobles para el trabajo manual y mecánico.

Descartados los experimentos manuales, la filosofía natural se basó en dos pilares puramente intelectuales: el razonamiento y la observación. El razonamiento permitía llegar a conclusiones basadas en la lógica, mientras que la observación de la naturaleza impedía que el razonamiento se alejara demasiado de la realidad. Con estas herramientas, el conocimiento griego y helenístico hizo grandes avances en disciplinas específicas, quedando estancado en otras. Fue muy grande el avance en matemáticas y lógica,  las cuales sólo necesitan de razonamiento. También el avance en astronomía y filosofía fue grande, pues esas disciplinas sólo necesitaban razonamiento y observación. Pero las disciplinas que necesitaban experimentos, como la física o la medicina, quedaron estancadas.

Después del estancamiento romano y de las edades oscuras que siguieron a la caída del Imperio, la filosofía natural medieval continuó y mejoró la filosofía natural griega en la que se basaba. Sin embargo, a pesar de que sentó las bases de la ciencia moderna, el amor por la teoría y desprecio por la práctica también limitó el alcance de esta filosofía natural medieval, que no pudo avanzar lo suficiente.

Galileo Galilei (1564​-1642) rescató al pensamiento occidental de este problema cuando, ya viejo y en arresto domiciliario decretado por la Inquisición, dejó de perder el tiempo y comenzó a hacer experimentos ingeniosos con el movimiento de los cuerpos, creando la ciencia y la Física modernas.

Pero el prejuicio contra lo manual continuó existiendo de forma más moderada, por inercia y porque es parte de la naturaleza humana. Al fin y al cabo, toda sociedad valora más al trabajo más intelectual, que está mejor remunerado. Así, se valora más al funcionario que al fontanero, al arquitecto que al obrero, al periodista que al que opera la prensa de un periódico, al profesor de Universidad que a la señora que limpia la Universidad.

De la misma manera, siempre se ha celebrado al científico teórico y pocas veces a aquel que crea los instrumentos (que muchas veces es también un científico). Galileo usó el telescopio para observar los cielos, pero no sabemos quien inventó el telescopio. Todos conocemos el nombre de Einstein, pero ¿conocemos el nombre de aquel que creó los instrumentos que se usaron para comprobar la teoría de la relatividad? Yo no lo conozco.

La historia de la Física está llena de grandes teóricos escritos con letras de oro: Copérnico, Kepler, Galileo, Newton, Maxwell, Einstein y todos los de la mecánica cuántica. ¿Se encuentran en los libros de historia de la Física los que crearon las máquinas con las cuales hacían los experimentos? Se menciona a unos pocos de paso y sin darles reconocimiento. Algunas veces quedan como notas a pie de página y la mayoría de veces ni se menciona. (Las excelentes series de televisión Conexiones 1, 2 y 3 de James Burke, disponibles en Youtube en español, recogen esos avances tecnológicos que quedan fuera de los libros de ciencia y a los que tanto debemos)

Un físico que trabaja en una Universidad o centro de investigación no quiere ser el personaje olvidado que creó los instrumentos que se usaron para comprobar las teorías de Einstein: quiere ser Einstein, alguien que es recordado y celebrado. Además, los físicos eligen la carrera porque les gusta la teoría. Si les gustara crear tecnología, serían ingenieros.

Sin aceleradores de partículas suficientemente potentes para llevar a cabo experimentos que distinguieran las teorías ciertas de las falsas, la Física se encontraba en graves problemas.

Si la estrategia anterior de construir aceleradores de partículas más potentes no resultaba factible, la segunda solución más razonable hubiera sido dejar de investigar en la unificación de fuerzas y pasar a otros temas. Había otros problemas menores en Física, que podían atacarse, aunque no eran tan atractivos como la unificación.

Y, si no se podía o no se quería resolver los problemas menores, se podía dejar reposar a la Física durante un tiempo (quizás siglos). A veces, pasa que una disciplina científica queda estancada durante un largo tiempo y no hay nada malo en ello.

Quizás con el tiempo se encontrara una solución al problema de la unificación. O quizás no existiera tal unificación y tendríamos que aceptar que hay tres tipos de fuerzas en el Universo (gravedad, fuerte, electrodébil) en vez de uno. Al fin y al cabo, que haya un único tipo de fuerzas en el Universo es una hipótesis, que puede ser cierta o falsa (yo no encuentro descabellado que la hipótesis sea falsa, pero esta es una posibilidad que no es ni siquiera considerada por la mayoría de los físicos, por una serie de aspectos no científicos que sería muy largo explicar aquí).

El problema es que no se podía dejar reposar la Física. La ciencia había sido un deber casi religioso hasta tiempos de Einstein y los científicos de la mecánica cuántica, los cuales, en su trabajo, se comportaban con una ética admirable y un amor a la verdad fuera de dudas. Pero en nuestra época se había convertido en una gran industria del que vivían millones de personas en universidades y centros de investigación. Muchos millones de dólares se dedicaban a la investigación científica. Mientras tanto, la cualidad moral de la sociedad (y, por tanto, del científico) había caído en picado. La ciencia era un gran negocio y la corrupción subió hasta extremos insospechados (para un análisis de este problema, ver el libro «Not even trying» de Bruce Charlton, disponible gratuitamente en línea).

Había que seguir con el negocio, costara lo que costara, pues muchos vivían de ello. Había que encontrar una solución. Y entonces, los físicos la encontraron, pero resultó ser una solución falsa que llevó al callejón sin salida actual.

3. La solución: volver a la Edad Media

Si no podemos comprobar teorías en base a experimentos, ¿por qué no comprobamos las teorías en base a su belleza matemática? La idea parecía razonable. Siempre los científicos han usado la belleza matemática para priorizar entre teorías.

En efecto, si una cosa nos han enseñado la filosofía natural y la ciencia, es que el Universo no se comporta al azar sino que es ordenado (es decir, sigue unas leyes).

Lo que se debería esperar si el Universo se hubiera generado por sí solo, es que las partículas del Universo se comportaran al azar, pues por cada comportamiento ordenado de una partícula, hay una cantidad inimaginable de comportamientos al azar de la misma partícula. Si esto lo multiplicamos por el número de partículas del universo, llegamos a una cantidad tan grande de comportamientos azarosos del Universo por cada comportamiento ordenado del Universo que no se puede expresar en términos matemáticos (por ejemplo, si se expresara de forma decimal 10000000….0000, el número de ceros sería inimaginablemente más grande que el número de electrones en el Universo).

No sólo el Universo sigue esas leyes , sino que estas leyes del Universo son de una gran belleza y coherencia matemática. Como descubrió Pitágoras en el siglo V a.C, el Universo está ordenado y este orden está escrito en lenguaje matemático. Este es el descubrimiento más importante de la historia de la ciencia. Siendo la matemática un producto del intelecto, resulta imposible evitar la conclusión de que la existencia de un diseñador inteligente del Universo, como han observado muchos científicos, incluido Einstein.

Es por ello que los científicos siempre han usado la belleza matemática como una orientación para llegar a una teoría científica. En efecto, dados unos datos (obtenidos de la observación o el experimento), hay infinitas teorías que podrían explicarlos, como se ve en la figura siguiente.

Dadas las infinitas teorías que concuerdan con los datos, ¿cómo elegir una? ¿cómo encontrar la que es cierta? ¿Cómo encontrar esa aguja única en un pajar infinito?

Normalmente, se intenta primero la que tiene más belleza matemática. Parte de esa belleza matemática es la simplicidad de la teoría. Este es el principio conocido como navaja de Occam (formulado por el monje católico y filósofo medieval inglés Guillermo de Occam, que vivió entre 1280 y 1349). La navaja de Occam dice «entre dos teorías que explican los datos, elige primero la más sencilla».

No es una regla que funcione siempre (como las reglas de la lógica que funcionan siempre). La navaja de Occam es una regla empírica («rule of thumb») que funciona bien la mayoría de las veces, como mínimo para una primera aproximación.

Por ejemplo, en la figura 6, aplicando la navaja de Occam, la teoría que se priorizaría sería la órbita en forma de elipse (es la más sencilla desde el punto de vista matemático). Sólo si los experimentos demuestran que es falsa, se considerarían otras teorías.

Sin embargo, el término «belleza matemática» no sólo contiene la simplicidad propuesta por Occam, sino también otros presupuestos estéticos subjetivos, lo que puede llevar a errores.

En otro ejemplo, Einstein formuló la teoría de la relatividad sólo con razonamientos y basándose en la belleza matemática de la teoría. Cuando le dijeron que su teoría se había comprobado en la observación de un eclipse dijo algo así como: «Mejor para la realidad, pues mi teoría es cierta» (cito de memoria).

Sin embargo, Einstein se equivocaba. Hay infinitas teorías bellas y sólo unas cuantas son ciertas. Es más: a veces la teoría que es cierta no es la más bella posible. Por ello, los experimentos son necesarios para distinguir una teoría cierta de la falsa.

Por ello, desde Galileo, el método de la física había sido siempre el siguiente:

• 1) Piensa en teorías posibles que puedan explicar los datos y, de todas las teorías que se te ocurren, elige la que tenga más belleza matemática.
• 2) Haz experimentos para obtener datos que te permitan comprobar o descartar esta teoría
• 3) Si se comprueba, ya has acabado. Si los datos de los experimentos la descartan, vuelve al punto 1), pero descartando esa teoría y todas las teorías que vayan en contra de los datos.

Lo que hicieron los físicos para salir del problema que tenían con la imposibilidad de hacer experimentos era prescindir de los pasos 2) y 3). La física se redujo al paso 1)

Es decir, la Física iba a prescindir de los experimentos e iba a volver a tiempos griegos y medievales, antes de Galileo, cuando todos los descubrimientos se hacían a puro trabajo intelectual, usando razonamiento y observación (pero no experimentos). Todo esto fue disimulado con el hecho de que se usaban complejas ecuaciones matemáticas, que daban respetabilidad al hecho de que la Física había dejado de ser ciencia y se había vuelto a convertir en filosofía natural (la cual había tenido éxitos, sin duda, pero que era limitada para un área como la física).

Esto impidió que la industria de la Física se parara. Los estudiantes podían hacer una tesis doctoral resolviendo un problema matemático de la teoría de cuerdas. Los profesores podían corregir estas tesis y pedir subvenciones para explorar detalles de la teoría de cuerdas. La física degeneró en un ejercicio puramente intelectual y matemático de expansión de teoría de cuerdas. Esto daba que comer a la gente, pero ya no era ciencia, sino una especie de ejercicio matemático, con poca relación con la realidad física. Todo ello se justificaba con el argumento que era un paso hacia la unificación de fuerzas o «teoría del todo», lo que, como hemos visto, es el Santo Grial de la Física moderna.

Pero lo peor todavía estaba por llegar y nos volvió a los peores momentos de la filosofía natural.

4. La historia de los epiciclos

Hemos dicho que la filosofía natural se basaba en razonamiento+observación, pero la ciencia se basa en razonamiento+observación+experimentos. Pero, ¿qué diferencia hay? ¿No es acaso la observación un caso especial de experimento?

En realidad, la línea que separa la observación del experimento es borrosa. El criterio principal es que un experimento está específicamente diseñado para comprobar o descartar la teoría que se está considerando. Es dependiente de la teoría que estamos analizando. Por el contrario, la observación es algo que ya está allí de forma independiente a la teoría que se está analizando (a veces, son datos obtenidos de experimentos diseñados para otras teorías). Es por eso que los experimentos obtienen datos más relevantes para evaluar si una cierta teoría es cierta.

No sólo eso, sino que las observaciones están dadas pero uno puede diseñar un número grande de experimentos en una pequeña cantidad de tiempo. Por eso, los experimentos obtienen más cantidad de datos para evaluar si una cierta teoría es cierta.

Sin los abundantes y relevantes datos de los experimentos, la física tiene difícil elegir entre teorías. Puede guiarse por criterios estéticos, de belleza matemática, pero esto puede llevarle a conclusiones inadecuadas.  Específicamente, cuando una observación descarta una teoría, existe la tendencia de complicar la teoría para que cumpla con los datos, sin cuestionar sus fundamentos básicos. Es más fácil reformar algo que tirarlo y comenzar de nuevo.

Nunca fue esto más evidente que con la teoría de cuerdas actual y con la astronomía de los siglos antes de Copérnico y Kepler. Platón había dicho que las órbitas de las planetas eran circulares y así se consideró por mucho tiempo. ¿Al fin y al cabo, no es el círculo la figura geométrica más bella en dos dimensiones (la más sencilla de describir matemáticamente)? El criterio de simplicidad no se había formulado (porque Occam no había nacido todavía) pero ya se estaba utilizando (de forma no sistemática).

Pero por la época de la Edad Media la tecnología de observación astronómica había avanzado y las observaciones astronómicas eran cada vez mejores y estaba claro que los planetas no se movían en círculos. La estrategia correcta hubiera sido rechazar la teoría de las órbitas circulares y empezar de nuevo.

Pero los pocos datos que había no justificaban un cambio tan radical. Así que los teóricos encontraron una salida, complicando la teoría para que se ajustara a los datos, sin cuestionar el círculo como fundamento básico. De esta manera, nació la teoría de los epiciclos.

Podemos ver esta teoría en la figura siguiente. Recordemos que estamos antes de Copérnico y se considera a la Tierra el centro del Sistema Solar.

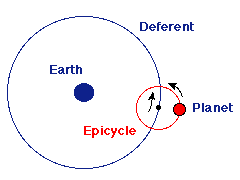
El planeta se mueve orbitando una pequeña orbita circular (que está en rojo en la figura), a la cual se le llama «epiciclo». El centro de este epiciclo (el punto negro) orbita a su vez alrededor de la Tierra en una gran órbita circular (que está en azul).

La combinación de estas dos órbitas circulares produce un movimiento combinado complejo del planeta, el cual vemos en la siguiente figura:

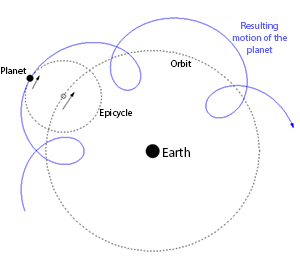
La línea en azul indica cómo se mueve el planeta cuando se combinan las dos órbitas circulares: la órbita grande y el pequeño epiciclo. Vemos que el movimiento es muy diferente a una órbita circular pero se ha producido a partir de dos órbitas circulares.

¿Para qué complicarse la vida de esta manera? Simplemente para reconciliar las observaciones astronómicas con el principio de que las órbitas son circulares.

Hemos visto en el apartado 3 que, cuando una observación u experimento falsea una teoría (por ejemplo, que las órbitas son circulares), hay que formular una nueva teoría. Pero, ¿cuál? Como he dicho, dada una serie de datos obtenidos por observación o experimentos, hay infinitas teorías que los explican. ¿Cómo elegir una entre las infinitas posibilidades?

 

Dadas las infinitas teorías que concuerdan con los datos, ¿cómo elegir una?. Como he dicho, el científico se guía por la belleza matemática. Muchas veces esto ha significado aplicar la navaja de Occam. Pero esta a veces resulta difícil de aplicarse y además a veces hay criterios de belleza diferentes de la simplicidad. Por ejemplo, los antiguos tenían muy arraigado el principio de que la Tierra era el centro y el principio platónico de que las órbitas eran circulares. Les resultaba inimaginable tirarlo todo y comenzar de nuevo.

Con los epiciclos podían tener las dos cosas: una teoría basada en el círculo y que explicaba los datos de las observaciones astronómicas.

Esto resolvió el problema por un tiempo. Sin embargo, la tecnología de observación astronómica seguía mejorando y, como consecuencia, las observaciones astronómicas eran cada vez más exactas.

En 1252 se publican las «Tablas alfonsíes», conjunto de observaciones astronómicas creadas a iniciativa de Alfonso X el Sabio (1221​- 1284), rey de Castilla y León. Las tablas indicaban la posición de los cuerpos celestes (Sol, Luna, planetas y estrellas) en el cielo de Toledo desde 1263 hasta 1272. Durante siglos fueron las tablas utilizadas para saber la posición de los cuerpos celestes en el cielo, lo que era de importancia vital para los navegantes, que se orientaban con las estrellas y que usaron estas tablas de forma intensiva.

A partir de las tablas alfonsíes, pronto se vio que el movimiento de los planetas no coincidía con el movimiento de la teoría de los epiciclos (que se ha dibujado en azul en la figura 9).

¿Qué hacer? Nosotros sabemos que lo razonable era poner al Sol en el centro del Sistema Solar y hacer las órbitas elípticas. Sin embargo, a los antiguos eso les parecía inimaginable, por lo que resolvieron el problema creando un segundo nivel de epiciclos, como se ve en la figura siguiente.

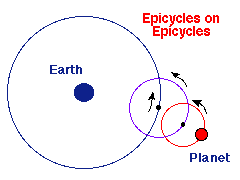
Ahora el planeta orbitaba sobre un pequeño epiciclo (en rojo), que a su vez orbitaba sobre un epiciclo grande (azul claro), que a su vez orbitaba en una órbita principal sobre la Tierra (azul oscuro).

Los astrónomos creían que, si jugamos con el tamaño y velocidad de cada órbita, podemos reproducir el movimiento del planeta sin desechar los principios de que la Tierra es el centro y las órbitas son circulares.

¿Y si no es así? No hay problema. Se podría crear un nivel más de epiciclos por cada planeta. En la figura 12, podemos colocar otro epiciclo sobre el círculo rojo y jugar con el tamaño y la velocidad hasta que coincida con las observaciones. ¿Y si no lo hace? Pues se puede poner otro nivel de epiciclos sobre ese anterior.

El problema es que esto es más fácil decirlo que hacerlo, pues la complejidad matemática de la teoría es muy grande y crece con el número de niveles de epiciclos. De hecho, los movimientos de los planetas y el Sol vistos desde la Tierra son los siguientes (recordemos que sólo se conocía hasta Saturno).

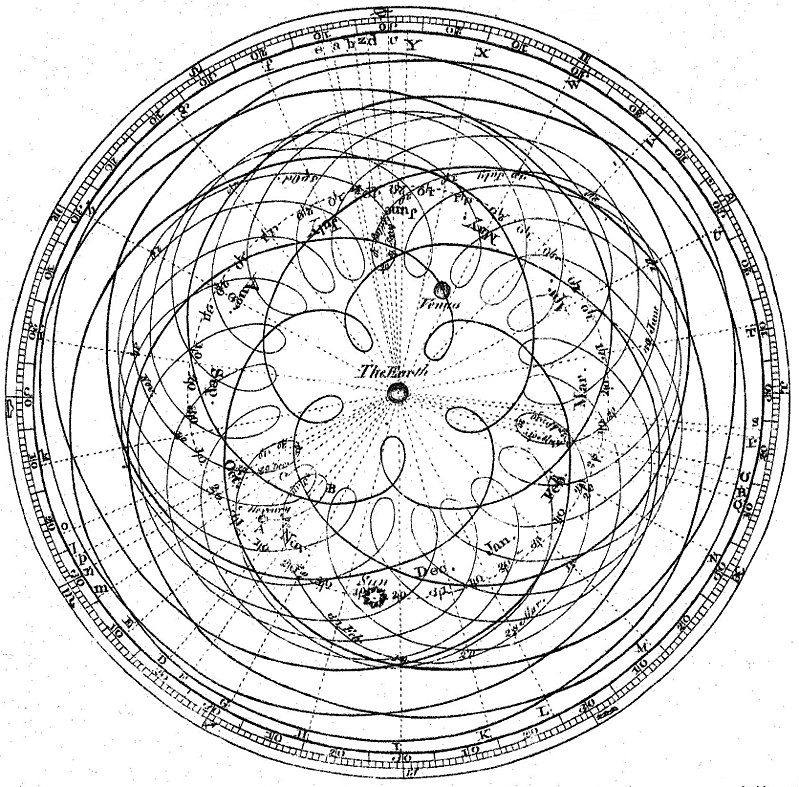
Crear un sistema de epiciclos que explicara estos complejos movimientos era de una gran complejidad matemática. Y esto en una época en que todos los cálculos se hacían a mano.

Cuando le enseñaron el sistema de epiciclos a Alfonso X el Sabio, comentó: «“Si Dios Todopoderoso me hubiera preguntado cuando hizo la creación, le hubiera recomendado algo más sencillo”.

Es fácil reírse de nuestros antepasados, que tuvieron que descubrir el camino que a nosotros se nos ha enseñado, pero veremos que una situación similar se da con la Física actual. En general, de la misma manera que los antiguos no podían ni imaginar que una órbita no fuera circular, nosotros no podemos ni imaginar que haya tres tipos de fuerzas en el Universo, en vez de una. Como veremos más adelante, esta idea fija está produciendo en la actualidad una complejidad mucho mayor que la teoría de los epiciclos. Así que no tenemos nada de lo que reírnos.

La historia de los epiciclos nos enseña dos cosas. La primera es que, si complicas suficiente la teoría, puedes demostrar cualquier cosa. De hecho, cuanto más compleja es la teoría, más variables o parámetros tienes (en nuestro caso, los parámetros son el tamaño y la velocidad de cada órbita). Por lo tanto, más combinaciones de parámetros son posibles y más comportamientos puedes explicar usando una combinación de estos parámetros.

Así, una teoría de una órbita circular sin epiciclos sólo puede demostrar movimientos circulares de los planetas. La teoría simple de epiciclos que se muestra en la figura 8 puede demostrar movimientos circulares (reduces el radio de cada epiciclo a 0 y lo tienes) y muchos otros movimientos más. La teoría de dos epiciclos por cada planeta es aún más general. De hecho, si añades suficientes epiciclos, puedes demostrar cualquier órbita.

La segunda lección es que el precio que debes pagar por una teoría que puede encajar con los datos reales sin abandonar supuestos básicos erróneos es que la teoría se hace cada vez más compleja y barroca.

Basándome en esta historia, llamaré «epiciclo» (entre comillas) a cualquier complicación de una teoría que se introduce para evitar el fracaso de esta teoría ante los datos de la realidad. Estos «epiciclos» hacen más compleja la teoría y hacen que sea más general, permitiéndole explicar más comportamientos posibles. Distinguir con la palabra epiciclos (sin comillas), que tiene el significado original de una órbita secundaria.

Como Alfonso X el Sabio, un monje católico polaco, Nicolás Copérnico (1473-1543)  se dio cuenta de que la teoría astronómica era demasiado compleja pero, al contrario del rey, decidió hacer algo. «Luego de realizar estudios sobre los griegos en Italia, este monje inicia la búsqueda de una explicación más sencilla, más simple, más de acuerdo con la naturaleza del Creador» («El búho de Minerva», Rafael Echeverría). Una explicación más bella, diría yo.

Copérnico puso el Sol en el centro del Sistema Solar, esperando simplificar este sistema endiablado y con la navaja de Occam se cargó a todos los epiciclos.

A partir de este sistema copernicano, el astrónomo Erasmus Reinhold publicó en 1551 las «Tablas prusianas», que los navegantes germanos utilizaron como mejora a las tablas alfonsíes, pero que no consiguieron llegar a toda Europa.

El problema del sistema copernicano es que se quedó a medias. Correctamente, Copérnico supuso que el Sol era el centro del Sistema Solar. Pero siguió suponiendo que las órbitas eran circulares, cuando son elípticas.

Seguro que la oscurantista Iglesia Católica lo condenó a la muerte por poner al Sol como centro del Sistema Solar. Por supuesto que no. Murió tranquilamente, la Iglesia lo enterró con todos los honores y sus teorías eran la moda en toda Europa y conversación animada entre los obispos y cardenales.

No se aceptó la teoría copernicana, simplemente porque la teoría no coincidía con las observaciones. Como los planetas se movían en órbitas elípticas y Copérnico decía que se movían en órbitas circulares, las predicciones hechas por la teoría copernicana no concordaban con las observaciones astronómicas. La teoría era falsa y era obvio que era falsa.

Aparecieron teorías intermedias, como las de Tycho Brahe, en que los planetas giraban alrededor del Sol y el Sol, a su vez, giraba alrededor de la Tierra. Todo estaba en ebullición y nada estaba seguro (un caso similar se da hoy en día con la génesis del Islam).

Este fue el problema de Galileo durante toda su vida. Galileo era un hombre de un orgullo intelectual enorme, que había colocado en la teoría de Copérnico. Quería obligar a la Iglesia a aceptar esta teoría, pero los obispos y cardenales decían que todavía no había suficiente evidencia y que, en el futuro, se podría reconsiderar si los datos la apoyaban. Después insultó veladamente al Papa (que había sido su mayor apoyo y aliado pero que era un hombre tan orgulloso como él) y todo se descontroló.

Al final, Johannes Kepler (1571 – 1630) dedicó toda su vida a resolver el problema. El astrónomo aficionado Tycho Brahe (1546 – 1601) había construido el mejor observatorio astronómico de toda Europa, inventando nuevas tecnologías de observación y guardando celosamente los datos de las observaciones sólo para él. Kepler se dirigió a su «corte» y esperó pacientemente por años. Sólo consiguió los datos cuando Brahe murió. Después se dedicó durante años a formular teorías y a demostrarlas haciendo cálculos a mano durante años. Su vida fue dura: huyendo de sitio en sitio en una Europa devastada por la guerra, su madre fue acusada de bruja y él empleó mucha energía en defenderla.

Devoto protestante, creía en la belleza matemática de un universo creado por Dios. Por ello, el día en que se dio cuenta de que las órbitas no eran circulares fue un día muy amargo para él. Comentó que sólo quedaban porquerías de figuras geométricas: parábolas, elipses… lejos del bello círculo. Al final, demostró que las órbitas eran elípticas (entre otras cosas). A partir de esta teoría y de las observaciones de Tycho Brahe, Kepler publicó las «Tablas Rudolfinas», que iban a sustituir a las tablas alfonsíes como guía de navegantes en todo el mundo.

Sin embargo, a pesar de la navaja de Occam, las teorías de Kepler tardaron mucho tiempo en aceptarse. Galileo y Descartes las ignoraron. Sólo Isaac Newton (1642-1727) consiguió hacerlas universales, al incorporarlas dentro de su teoría de la gravedad, que explicaba el motivo de las órbitas elípticas.

5. La Física actual es un juego de epiciclos

¿Por qué me he desviado tanto del tema principal para contar esta parte de la historia de la ciencia? Porque creo que la Física se encuentra ahora en un momento similar al de los epiciclos. La teoría de los epiciclos actual de la Física es la «teoría de cuerdas», que ya hemos visto.

Como habíamos visto en el apartado 3, la Física se ha convertido en una filosofía natural alejada de los experimentos: un ejercicio teórico disimulado por el uso de lenguaje matemático. Los físicos ya no hacen ecuaciones y comprueban que son ciertas usando experimentos. Ahora hacen ecuaciones y deciden que son ciertas basándose en su belleza matemática.

Esto es peligroso, pues la física no es una disciplina puramente teórica, como las matemáticas o la lógica. Desde Galileo, que la fundó, la física ha sido una disciplina basada en los experimentos. Sin ellos, la física tiene tendencia en caer en problemas parecidos a la teoría de epiciclos que acabamos de ver.

Esto pasó con la teoría de cuerdas. La idea de que las partículas eran líneas vibrantes («cuerdas») y que esta vibración podía explicar todo el universo físico y unificar todas las fuerzas resultó ser tan seductora para los físicos actuales como la idea de que las órbitas eran circulares para los astrónomos medievales.

Pasó lo mismo que en tiempos medievales: cada vez que una observación desmentía las órbitas circulares, simplemente se complicaba la teoría añadiendo una complicación o epiciclo más para que la teoría concordara con las observaciones y mantener el fundamento circular que tanto se amaba.

Con la teoría de cuerdas pasó lo mismo. Aunque la teoría no podía comprobarse con experimentos, sí que había datos obtenidos con otros experimentos físicos con los que tenía que concordar (podríamos considerarlos análogos a las observaciones astronómicas de la teoría de epiciclos).

Pronto se vio que la teoría de cuerdas no concordaba con estas observaciones. Pero ya los físicos se habían enamorado de la física de cuerdas y no la iban abandonar tan fácilmente, de la misma forma que los astrónomos medievales se resistieron a abandonar el círculo.  Este enamoramiento se basa en parte en cuestiones prácticas (en parte porque los científicos son reacios a abandonar una teoría en la que han trabajado por toda su vida y empezar de nuevo) y también en cuestiones teóricas (algunos físicos con poco conocimiento filosófico habían hecho de una teoría de este estilo la base de sus concepciones filosóficas deficientes).

¿Qué hacer cuando no quieres abandonar una teoría pero quieres que concuerde con los experimentos que la desmienten? Siempre puedes añadir un «epiciclo», una complicación de la teoría que le permite explicar más comportamientos y que, por lo tanto, pueda explicar los comportamientos que has obtenido de las observaciones. Si añades suficientes «epiciclos», puedes justificar cualquier cosa.

En la teoría de cuerdas, los primeros «epiciclos» consistieron en añadir dimensiones espaciales. Como sabemos, el Universo tiene tres dimensiones espaciales y una temporal. De repente, se dijo que, en realidad, el Universo constaba de ocho, diez, once o doce dimensiones espaciales (dependiendo la versión de la teoría). No era un impedimento que estas dimensiones no se habían detectado: se dijo que eran microscópicas e indetectables y, de todas maneras, lo importante es que las ecuaciones matemáticas cuadraran. Añadiendo más dimensiones podías explicar más comportamientos posibles: entre ellos, los que se habían observado. Esta era la situación durante los años ochenta, en que yo estudiaba.

Pronto esto se reveló insuficiente, pues los datos no cuadraban con estas teorías primeras, ni incluso añadiendo varias dimensiones. Lo razonable hubiera sido desechar la teoría, pero como hemos dicho, los físicos amaban demasiado la teoría de cuerdas. Se solucionó añadiendo más «epiciclos» a la teoría. Volviéndola a complicar para añadirle más parámetros y, por lo tanto, poder explicar más comportamientos posibles. Así nació la teoría de supercuerdas (o supersimetría o SUSY) que, como habrás supuesto, falló en obtener ninguna comprobación experimental (pero dio de comer a mucha gente).

Pero los físicos siguieron haciendo ecuaciones sin desanimarse por ello. Como consecuencia, aparecieron seis versiones de la teoría de supercuerdas, llamadas:

• La Teoría de supercuerdas de Tipo I.
• La Teoría de supercuerdas de Tipo IIA.
• La Teoría de supercuerdas de Tipo IIB.
• La Teoría de supercuerdas heterótica SO(32).
• La Teoría de supercuerdas heterótica E8xE8.
• La Teoría de supercuerdas supergravedad 11D

En 1995, Edward Witten demostró que estas seis versiones eran casos particulares de una teoría más general llamada «teoría M» («M-theory»). Como se ve, la teoría M es más general que cualquiera de estas teorías de supercuerdas y, por lo tanto, es más complicada, tiene más parámetros y permite explicar más comportamientos posibles.

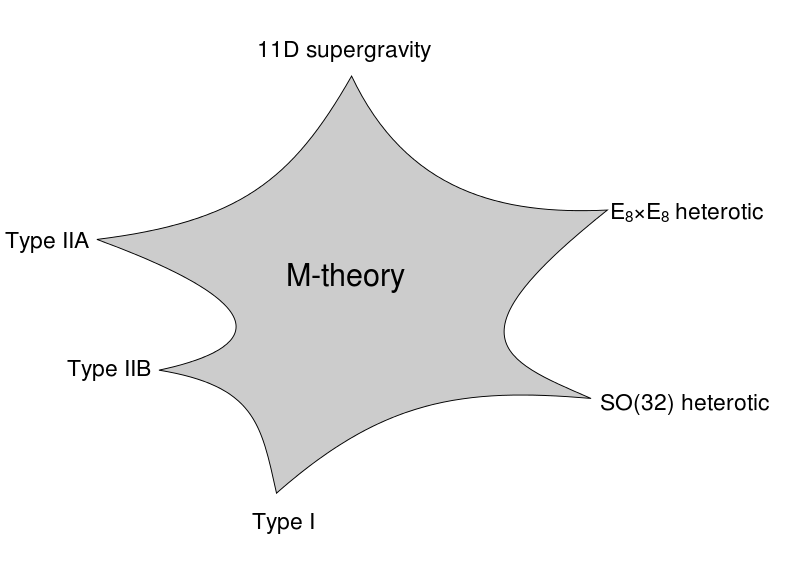
¿En qué se basa la «teoría M»? En este contexto, «M» significa «membrana». Al contrario que la teoría de cuerdas clásicas (que suponía que las partículas eran líneas unidimensionales que vibraban), la teoría M supone que las partículas son planos o membranas, objetos bidimensionales que vibran. Obviamente, una línea es un caso específico de un plano, por lo que las membranas permiten explicar más cosas que las cuerdas. Se trata, en suma, de otro «epiciclo» que permite explicar más comportamientos al precio de complicar la teoría.

En todo este proceso, la matemática se hizo cada vez más compleja e inmanejable. Pronto, cada «avance» en teoría de cuerdas constaba de cientos de páginas con abstrusas ecuaciones. Como la teoría era cada vez más compleja, tenía cada vez más parámetros y era difícil saber qué combinación de parámetros era la cierta.

Uno imagina a Alfonso X el Sabio resucitando y diciendo a los teóricos de cuerdas: “Si Dios Todopoderoso me hubiera preguntado cuando hizo la creación, le hubiera recomendado algo más sencillo”.

A falta de un rey medieval, otros han dado la voz de alarma, en 2006, Peter Woit, Doctor en Física Teórica y profesor de matemáticas en la Universidad de Columbia publica el artículo «Not Even Wrong: The Failure of String Theory and the Search for Unity in Physical Law«, que acaba convirtiéndose en un libro. En junio de 2018, está prevista la publicación de «Lost in Math: How Beauty Leads Physics Astray» de Sabine Hossenfelder. El texto de la solapa no puede ser más aclarador:

Ya se considerando los agujeros negros o prediciendo descubrimientos en el CERN, los físicos creen que las mejores teorías son bellas, naturales y elegantes y que este criterio separa las teorías populares de las que se desecha.  Sabine Hossenfelder afirma que esta es la razón de que no hayamos visto un avance importante («major breakthrough») en los fundamentos de la Física durante más de cuatro décadas.

La creencia en la belleza se ha hecho tan dogmática que ahora entra en conflicto con la objetividad científica: la observación ha sido incapaz de confirmar teorías excitantes, como supersumetría o la gran unificación, inventadas por los físicos basándose en criterios estéticos.

Aún peor, esas teorías «demasiado buenas para no ser ciertas» son imposibles de comprobar en la realidad y han dejado la disciplina en un callejón sin salida. Para escapar, los físicos deben replantearse sus métodos. Sólo aceptando la realidad como es puede la ciencia descubrir la verdad.

Como el texto anterior afirma, se sabe que la teoría de cuerdas no es falsificable. Es decir, que no hay ningún experimento concebible que pudiera demostrar que es falsa. Así, por ejemplo, la teoría de la gravedad de Einstein es falsificable, pues se podría imaginar un movimiento que no se ajustara a las ecuaciones de la teoría, lo que demostraría que la teoría es falsa («falsificaría la teoría»).

Que la teoría de cuerdas no es falsificable es consecuencia de lo que contaba anteriormente: la teoría se ha hecho tan compleja y con tantos parámetros que puede explicar cualquier cosa (de la misma que una teoría con suficiente número de epiciclos podía explicar cualquier movimiento planetario). De forma que ningún experimento puede descartarla, pues cualquier observación es compatible con la teoría.

Que la teoría de cuerdas no sea falsificable es importante, pues, desde Karl Popper, se ha supuesto que una teoría que no es falsificable, no es una teoría científica. Los teóricos de cuerdas se defienden diciendo que hay que redefinir el concepto de ciencia, para que incluya teorías no falsificables por experimentos. A estos extremos lamentables hemos llegado.

Otros menos radicales dicen que, aunque la teoría de cuerdas no es falsificable, lo puede ser en el futuro. Pero en el futuro, puede pasar cualquier cosa y no es ningún argumento válido «el futuro me dará la razón», que todo el mundo puede decir para sostener su posición.

Mientras tanto, la teoría de cuerdas ha llegado al gran público. Los libros de divulgación científica la presentan como cierta a un público incauto, a pesar de no contar con ninguna evidencia. Los más importantes de estos libros incluyen «El universo elegante» (1999) por Brian Greene o «El gran diseño» (2010) por Stephen Hawking y Leonard Mlodinow.

El 21 de junio de 2000, en una reunión de físicos en Copenhaguen, se formuló una apuesta (llamada «SUSY bet») bajo la pregunta: «¿Cree usted que en 10 años se habrá descubierto experimentalmente «una pareja supersimétrica de una partícula conocida»? (es decir, una partícula que demuestre que una teoría de las supercuerdas es cierta). Esta apuesta (que involucraba una botella de coñac) se renovó en 2011. En 2016, cuando no se descubrió nada, los perdedores pagaron deportivamente la botella, pero no renunciaron a la teoría de cuerdas, que se ha vuelto una pared que está bloqueando el avance de la física.

Es difícil saber que hacer ante este callejón sin salida de la Física actual. La mayoría de físicos siguen diciendo que hay que seguir con la teoría de cuerdas y que, aunque no hay evidencias, debemos esperar pacientemente a que los dé. Si hace falta, esperar siglos. Uno recuerda la teoría de epiciclos que detuvo la teoría astronómica por siglos sin ninguna evidencia.

Uno de los perdedores de la apuesta «SUSY bet» (David Gross) dijo lo siguiente:

En la ausencia de alguna evidencia experimental positiva de la supersimetría, es un buen momento para aterrorizar a los jóvenes en el público y decirles: «No seguid a vuestros mayores…Id y buscad algo nuevo y loco y poderoso y diferente. Especialmente, diferente. Definitivamente, esta es una buena lección. Pero soy demasiado viejo para ello.

Palabras sabias, sin duda. Sin embargo, no llegan al fondo del asunto, que es la dificultad de comprobar las teorías con experimentos, dadas las inmensas energías que se necesitan. Sin los experimentos, cualquier teoría «nueva y loca y poderosa y diferente», acabará siendo otra teoría matemática que añada «epiciclos» y «epiciclos» hasta convertirse en un maremágnum parecido a la teoría de cuerdas actual. Sin experimentos, la física no puede avanzar.

Mi predicción es que, de la misma manera que se pasaron siglos con la teoría de los epiciclos, pasaremos mucho tiempo con la física en punto muerto, con los físicos ganándose el pan formulando versiones más complejas de teorías matemáticas sin relación con la realidad y diciendo que la unificación está a la vuelta de la esquina. Hemos entrado en una segunda época de los epiciclos.

En última instancia, lo que hizo desechar la teoría de los epiciclos y adoptar la teoría de Copérnico-Kepler no fue la idea de que el Sol podía estar en el centro, lo cual ya había sido propuesto por Aristarco de Samos (310 – 230 a.C). Lo que acabó con la teoría de los epiciclos fueron las observaciones astronómicas cada vez más exactas que se estaban dando en la Edad Media y el Renacimiento. Las tablas alfonsinas o las observaciones de Tycho Brahe fueron las que hicieron que los modelos teóricos no tuvieran más remedio que variar. Y estas observaciones eran consecuencia de una tecnología de observación astronómica cada vez más avanzada. Fue la tecnología la que hizo avanzar la ciencia y la que hizo desechar teorías demasiado complejas para acercarse a la verdad.

De la misma manera, cuando la tecnología de aceleradores de partículas avance y permita comprobar las teorías de unificación, la Física saldrá de las arenas movedizas actuales (similares a la teoría de epiciclos) y hará un progreso hacia adelante. Pero seguramente nosotros ya no veremos esto. Para nosotros, la Física ha entrado en una segunda era de los epiciclos, en un callejón sin salida.